1.11 – Practice Problem 1

Question

In wastewater treatment, an important step in the process is sedimentation. Sedimentation is the process of allowing particulate matter in a fluid to settle to the bottom of a tank. In the sedimentation step, a coagulant can be used to coagulate bacteria and fine particles to allow the sedimentation to occur faster. The most common molecular species used for coagulation is alum, \(Al_2 (SO_4)_3 \cdot 14H_2 O\).

You are a chemical engineer working in a waste water treatment plant. You are asked to make a material balance on the sedimentation process. Waste water flows into a sedimentation tank at 200 kg/s. The waste water contains 0.01 wt% of bacteria, 2 wt% particulate matter, and the balance pure water. Pure alum is added to the sedimentation tank in a separate stream. Alum allows 80% of the bacteria and 100 % of the particulate matter to settle. Just enough alum is added for this ratio of settlement. The sludge at the bottom of the tank exits the tank with 20 wt% of water and 40 wt% of particulate matter. The semi-treated water exits the tank in a separate stream.

1. Draw and label a block flow diagram (BFD).
2. Perform a degree of freedom analysis.
3. Fully balance the remainder of the block flow diagram.

Answer

a) Draw and label a block flow diagram (BFD)

First, let’s draw the basic layout of the BFD:

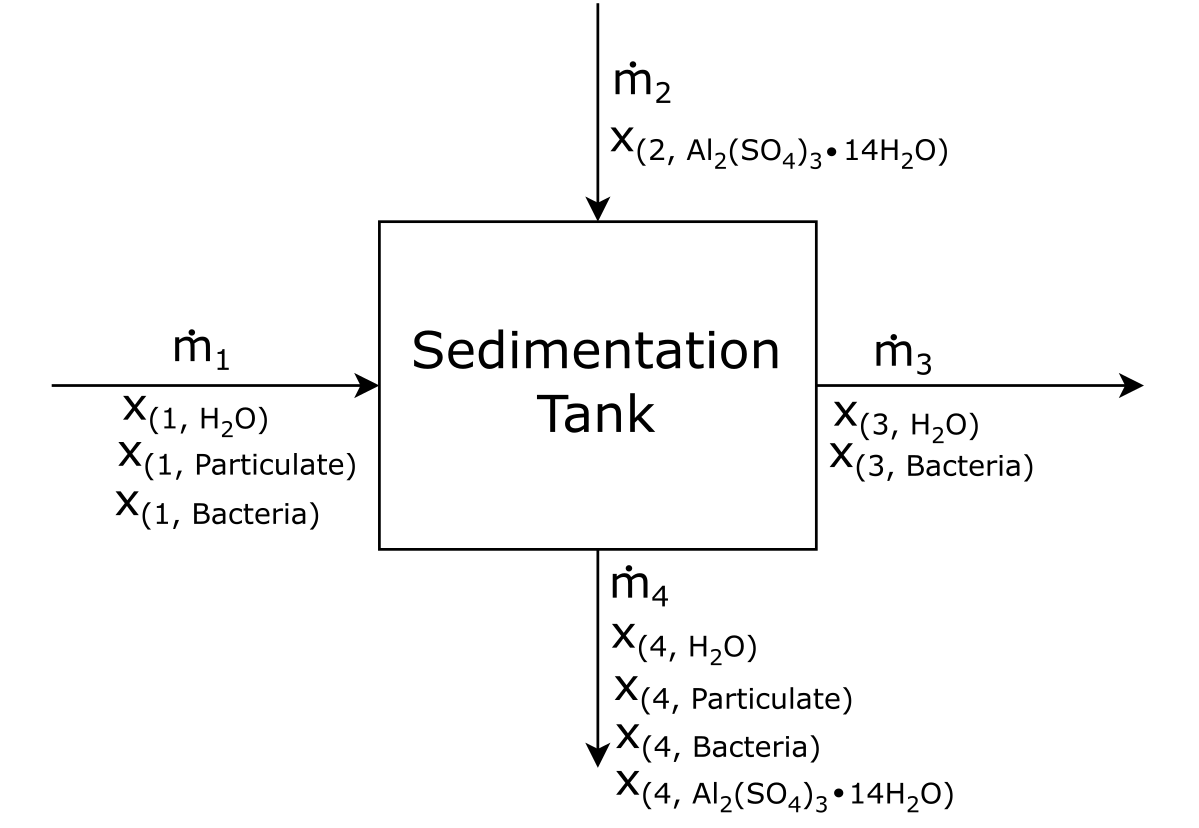
Attribution: Said Zaid-Alkailani & UBC [CC BY 4.0 de (https://creativecommons.org/licenses/by/4.0/)]

Using the information given, let’s fill out as much of the BFD as we can.

\[x_{(1, \space H_2 O)} = 1 - x_{(1, \space Particulate)} - x_{(1, \space Bacteria)} = 1 - 0.02 - 0.0001 = 0.9799\]

\[x_{(2, \space Al_2 (SO_4)_3 \cdot 14 H_2 O)} = 1\]

\[x_{(4, \space H_2 O)} = 0.20\]

\[x_{(4, \space Particulate)} = 0.40\]

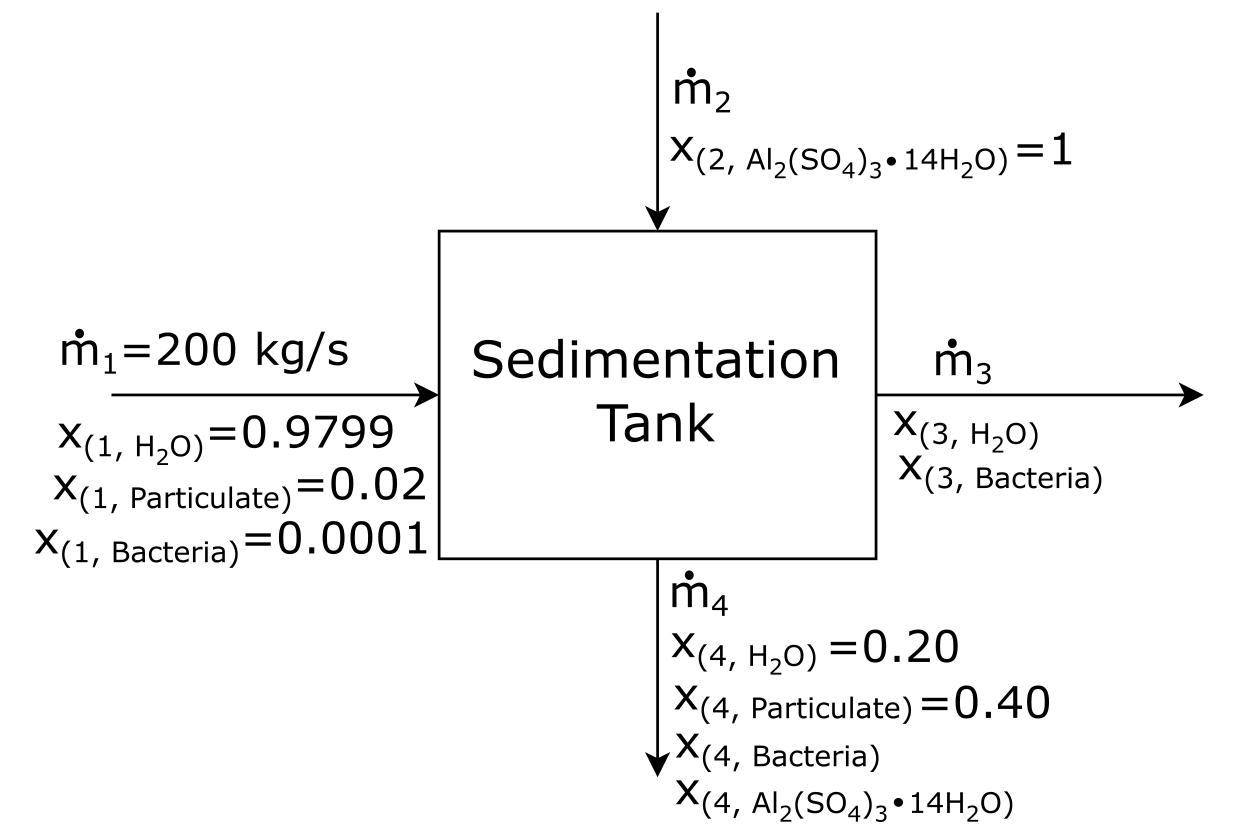
Attribution: Said Zaid-Alkailani & UBC [CC BY 4.0 de (https://creativecommons.org/licenses/by/4.0/)]

b) Perform a degree of freedom analysis

We have 7 unknowns, so we need to find 7 equations. First lets do all of the mass balances:

\[\dot{m}_1 x_{(1, \space H_2 O)} = \dot{m}_3 x_{(3, \space H_2 O)} + \dot{m}_4 x_{(4, \space H_2 O)}\]

\[\dot{m}_1 x_{(1, Particulate)} = \dot{m}_4 x_{(4, Particulate)}\]

\[\dot{m}_1 x_{(1, Bacteria)} = \dot{m}_3 x_{(3, Bacteria)} + \dot{m}_4 x_{(4, Bacteria)}\]

\[\dot{m}_2 x_{(2, \space Al_2 (SO_4)_3 \cdot 14 H_2 O)} = \dot{m}_4 x_{(4, \space Al_2 (SO_4)_3 \cdot 14 H_2 O)}\]

Now lets do the mass fraction balance:

\[x_{(3, \space H_2 O)} = 1 - x_{(3, Bacteria)}\]

\[x_{(4, \space Particulate)} = 1 - x_{(4, H_2 O)} - x_{(4, Bacteria)} - x_{(4, \space Al_2 (SO_4)_3 \cdot 14 H_2 O)}\]

Next lets write our the extra equation:

\[0.80 \cdot \dot{m}_1 x_{(1, Bacteria)} = \dot{m}_4 x_{(4, Bacteria)}\]

Finally we can solve for the degrees of freedom:

\[\text{DOF} = 7 - 7 = 0\]

c) Fully balance the remainder of the block flow diagram

To fully we balance the diagram we must first solve for all of the unknowns.

1. Solve for \(\dot{m}_4\) using particulate balance:

\[\dot{m}_1 x_{(1, Particulate)} = \dot{m}_4 x_{(4, Particulate)}\]

\[\dot{m}_4 = \frac{\dot{m}_1 x_{(1, Particulate)}}{x_{(4, Particulate)}} = \frac{(200)(0.02)}{0.4} \space \frac{kg}{s} = 10 \space \frac{kg}{s}\]

2. Solve for \(x_{(4, Bacteria)}\) using the extra equation:

\[0.80 \cdot \dot{m}_1 x_{(1, Bacteria)} = \dot{m}_4 x_{(4, Bacteria)}\]

\[x_{(4, Bacteria)} = \frac{0.80 \cdot \dot{m}_1 x_{(1, Bacteria)}}{\dot{m}_4} = \frac{\big( 0.80 \big) \big( 200 \space \frac{kg}{s} \big) \big(0.0001 \big)}{10 \space \frac{kg}{s}} = 0.0016\]

3. Solve for \(x_{(4, \space Al_2 (SO_4)_3 \cdot 14 H_2 O)}\) using the fractional mass balance:

\[x_{(4, \space Al_2 (SO_4)_3 \cdot 14 H_2 O)} = 1 - x_{(4, H_2 O)} - x_{(4, Bacteria)} - x_{(4, \space Particulate)} = 1 - 0.20 - 0.0016 - 0.40 = 0.3984\]

4. Solve for \(\dot{m}_2\) using the alum balance:

\[\dot{m}_2 x_{(2, \space Al_2 (SO_4)_3 \cdot 14 H_2 O)} = \dot{m}_4 x_{(4, \space Al_2 (SO_4)_3 \cdot 14 H_2 O)} = \bigg(10 \space \frac{kg}{s} \bigg) \bigg(0.3984 \bigg) = 3.984 \space \frac{kg}{s}\]

5. Solve for \(\dot{m}_3\) using a combination of the water balance and bacteria balance:

\[\dot{m}_1 x_{(1, Bacteria)} = \dot{m}_3 x_{(3, Bacteria)} + \dot{m}_4 x_{(4, Bacteria)}\]

\[\dot{m}_3 = \frac{ \dot{m}_1 x_{(1, \space Bacteria)} - \dot{m}_4 x_{(4, \space Bacteria)}}{x_{(3, \space Bacteria)}}\]

\[\dot{m}_1 x_{(1, \space H_2 O)} = \dot{m}_3 x_{(3, \space H_2 O)} + \dot{m}_4 x_{(4, \space H_2 O)}\]

\[\dot{m}_3 = \frac{ \dot{m}_1 x_{(1, H_2 O)} - \dot{m}_4 x_{(4, H_2 O)}}{x_{(3, H_2 O)}}\]

We can equate these two equations to get:

\[\frac{ \dot{m}_1 x_{(1, \space Bacteria)} - \dot{m}_4 x_{(4, \space Bacteria)}}{x_{(3, \space Bacteria)}} = \frac{ \dot{m}_1 x_{(1, H_2 O)} - \dot{m}_4 x_{(4, H_2 O)}}{x_{(3, H_2 O)}}\]

and using the fractional mass balance

\[x_{(3, \space H_2 O)} = 1 - x_{(3, \space Bacteria)}\]

we can solve for \(x_{(3, \space Bacteria)}\)

\[\frac{ \dot{m}_1 x_{(1, \space Bacteria)} - \dot{m}_4 x_{(4, \space Bacteria)}}{x_{(3, \space Bacteria)}} = \frac{ \dot{m}_1 x_{(1, H_2 O)} - \dot{m}_4 x_{(4, H_2 O)}}{1 - x_{(3, \space Bacteria)}}\]

\[\frac{0.004}{x_{(3, \space Bacteria)}} = \frac{193.98}{1 - x_{(3, \space Bacteria)}}\]

\[x_{(3, \space Bacteria)} = 0.00002\]

\[\therefore \space x_{(3, \space H_2 O)} = 1 - 0.00002 = 0.99998\]

\[\therefore \space \dot{m}_3 = \frac{ \dot{m}_1 x_{(1, H_2 O)} - \dot{m}_4 x_{(4, H_2 O)}}{x_{(3, H_2 O)}} = \frac{ 193.98 }{0.99998} \space \frac{kg}{s} = 193.98 \space \frac{kg}{s}\]

Now that we have completely solved the material balance, we can complete our BFD:

Attribution: Said Zaid-Alkailani & UBC [CC BY 4.0 de (https://creativecommons.org/licenses/by/4.0/)]